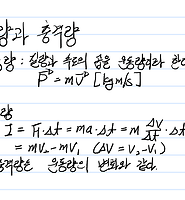| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 7급
- 공무원
- 와전류
- 아이엠게스트하우스
- 표선이래하우스
- 기술직
- 배알도수변공원
- 청년게스트하우스
- 괴강교
- Segara Beach
- 행촌교차로
- 백로공원
- 담양시내
- 무심천교
- 합강공원
- 익산성당포구
- 침투깊이
- 횡탄정
- 해거름마을공원
- 이포보
- 백패커스게스트하우스
- 쓰담쓰담게스트하우스
- 또또게스트하우스
- 법환바당
- 영산강하굿둑
- 골드스텔라호
- 미나리깡
- 게스트하우스305
- 여수엑스포여객선터미널
- 느러지관람전망대
- Today
- Total
베르스퍼의 일상
[이론] 힘과 운동 / 만유인력 본문
만유 인력
- 만유인력의 법칙
$$ F = G { m_1 m_2 \above 1pt r^2 } (만유인력 \space 상수(G) \space : \space 6.67\cdot 10^-11 N\cdot m^2 / {kg}^2) $$
- 중력
$$ F = G{Mm \above 1pt r^2} = mg\space , \space g = G\cdot {M \above 1pt R^2}{(지구\space 중량) \atop (지구\space 반지름)} $$
- 지구 내부에서의 중력
$$ g = G\cdot {M \above 1pt R^2}\space\space\space(\rho = {M \above 1pt V} = {M \above 1pt {4 \above 1pt 3} \pi R^3} )$$
$$ g = G\cdot {M \above 1pt R^2} = {G \above 1pt R^2} \cdot { 4 \above 1pt 3} \rho \cdot \pi R^3 = {4 \above 1pt 3} G\rho\pi R (g \varpropto R) $$
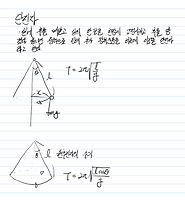
- 지구 중심을 지나는 단진동 물체의 주기
|
$$ T = 2\pi\sqrt{R^3 \above 1pt GM} $$ 주기 $T$는 $r$에 상관없이 일정 |
- 지표 근처에서 원운동 하는 인공위성의 속도
|
$$ 만유인력=원심력={GMm \above 1pt (R+h)^2} = {mv^2 \above 1pt R+h}$$ $$ v^2 = {GM \above 1pt R+h} = {GM \above 1pt r}(R+h = r)$$ $$={GM \above 1pt r^2} \cdot r \left(R\gg r 이므로 {GM \above 1pt r^2} \approx {GM \above 1pt R^2}\right) $$ $$=gr \left( {GM \above 1pt R^2} = g \right)$$ $$ v = \sqrt{gr}$$ |
- 고도 h가 충분히 클 경우의 주기 T
$$ v = \sqrt{GM \above 1pt R+h} = (R+h)\omega = (R+h)\cdot {2\pi \above 1pt T}$$
$$ {GM \above 1pt R+h }=(R+h)^2 \cdot {(2\pi)^2 \above 1pt T^2}$$
$$ T^2 = {(2\pi)^2 \above 1pt GM} \cdot (R+h)^3, \space\space\space T^2 \varpropto (R+h)^3$$
$$= {(2\pi)^2 \above 1pt gR^2}(R+h)^3, \space \space\space \left( {GM \above 1pt R^2} = g \right)$$
'물리학개론(이론정리) > 힘과 운동' 카테고리의 다른 글
| [이론] 힘과 운동 / 운동량 보존의 법칙 (0) | 2018.06.01 |
|---|---|
| [이론] 힘과 운동 / 운동량과 충격량 (0) | 2018.06.01 |
| [이론] 힘과 운동 / 단진자 (0) | 2018.06.01 |
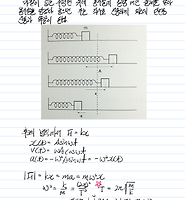
| [이론] 힘과 운동 / 용수철 진자 (0) | 2018.06.01 |
| [이론] 힘과 운동 / 단진동 (0) | 2018.06.01 |